What Is 6/7 - 2/5
Multiplying Fractions
Nosotros will discuss here about multiplying fractions by a whole number, by a fractional number or by another mixed partial number.
I. Multiplication of Fractional Number past a Whole Number:
We accept learnt 4 × 5 = 4 times v
= 5 + five + v + 5
= 20
In the same way 6 × \(\frac{i}{7}\) = 6 times \(\frac{ane}{7}\)
= \(\frac{1}{7}\) + \(\frac{1}{7}\) + \(\frac{ane}{7}\) + \(\frac{one}{seven}\) + \(\frac{ane}{7}\) + \(\frac{i}{seven}\)
= \(\frac{ane + 1 + 1 + 1 + 1 + 1}{7}\)
= \(\frac{half dozen}{vii}\)
i.east., six × \(\frac{1}{vii}\) = \(\frac{6 × 1}{7}\) = \(\frac{six}{7}\)
Multiply four × \(\frac{3}{five}\)
4 × \(\frac{3}{five}\) = 4 times 4 × \(\frac{three}{five}\)
= \(\frac{three}{v}\) + \(\frac{iii}{5}\) + \(\frac{3}{5}\) + \(\frac{3}{5}\)
= \(\frac{12}{5}\)
i.due east. four × \(\frac{3}{5}\) = \(\frac{iv × 3}{5}\) = \(\frac{12}{5}\)
Production of a whole number and a fractional number =
\(\frac{\textrm{Product of Whole Number × Numerator of the Fractional Number}}{\textrm{Denominator of the Partial Number}}\)
For examples:
\(\frac{three}{iv}\) × 5 = \(\frac{3 × 5}{4}\) = \(\frac{15}{4}\)
\(\frac{6}{7}\) × 2 = \(\frac{half-dozen × ii}{7}\) = \(\frac{12}{7}\)
7 × \(\frac{4}{5}\) = \(\frac{7 × 4}{5}\) = \(\frac{28}{5}\)
iv × \(\frac{three}{11}\) = \(\frac{4 × 3}{11}\) = \(\frac{12}{eleven}\)
Permit united states of america multiply \(\frac{1}{4}\) by 3. We utilise the rule of repeated improver to discover the product.

We can say that \(\frac{1}{iv}\) of 3 = \(\frac{iii}{4}\)
To multiply a fraction by a whole number, nosotros multiply the numerator of the fraction past the whole number and reduce the fraction to the lowest terms, if and so required.
For example:
(i) Multiply 1\(\frac{2}{9}\) by 25
Solution:
1\(\frac{2}{9}\) × 25
= \(\frac{ane × ix + ii}{9}\)
= \(\frac{11}{9}\) × 25
= \(\frac{11 × 25}{9}\)
= \(\frac{275}{nine}\)
= xxx\(\frac{five}{ix}\)
| (2) Multiply 2/3 by vii Solution: two/3 × 7 = (2 × vii)/3 = 14/3 = 4 2/3 | We simply multiply the numerator of the fractional number past the whole number. The denominator remains the aforementioned. |
| (iii) Multiply xx × \(\frac{4}{5}\) 20 × \(\frac{iv}{5}\) = \(\frac{20 × iv}{5}\) = \(\frac{2 × 2 × \not five × 2 × 2}{\not 5}\) = 16 | xx = 2 × 2 × 5 4 = 2 × ii five = five × 1 |
| (iv) Multiply ii\(\frac{3}{5}\) by 6 Solution: 2\(\frac{3}{5}\) × 6 = (2 × 5 + 3)/v × 6 = (10 + iii)/v × 6 = xiii/five × six = (13 × half dozen)/5 = 78/five = 15\(\frac{3}{5}\) | We modify the mixed numbers into improper fractions and then just multiply the numerator of the fractional number by the whole number. The denominator remains the same. |
Ii. Multiplication of Fractional Number past Another Fractional Number:
For example:
| (i) Multiply 2/five past four/5 Solution: two/5 × four/5 = (2 × 4)/(5 × v) = 8/25 | Step I: We multiply the numerators. Step Two: We multiply the denominators. Footstep III: We write the fraction in the simplest course. |
| (ii) Multiply 8/ix by 7/10 Solution: 8/9 × 7/ten = (viii × vii)/(9 × 10) = 56/90 | We simply multiply the numerators of the fractional numbers and and then multiply the denominators of the fractional numbers. Write the fraction in the simplest form. |
(iii)Multiply \(\frac{four}{7}\) × \(\frac{2}{5}\)
Multiply the numerators to get the numerator of the product and
Multiply the denominators to get the denominator of the product.
Reduce the product to the lowest terms.
Therefore, \(\frac{iv}{7}\) × \(\frac{two}{v}\) = \(\frac{4 × two}{seven × 5}\) = \(\frac{8}{35}\)
Iii: Production of More than 2 Fractions:
For examples:
(i) Multiply \(\frac{9}{x}\) × \(\frac{2}{5}\) × \(\frac{3}{vii}\)

Method I: \(\frac{9}{10}\) × \(\frac{2}{5}\) × \(\frac{3}{seven}\) = \(\frac{9 × 2 × 3}{10 × 5 × 7}\) = \(\frac{54}{350}\)
H.C.F. of 54 and 350 is 2
\(\frac{54 ÷ 2}{350 ÷ 2}\) = \(\frac{27}{175}\)
Therefore, \(\frac{nine}{10}\) × \(\frac{2}{5}\) × \(\frac{three}{7}\) = \(\frac{27}{175}\)
Method II: \(\frac{9}{x}\) × \(\frac{ii}{5}\) × \(\frac{iii}{seven}\) = ?
| 9 = 3 × 3 2 = 2 × 1 3 = 3 × 1 | 10 = 2 × 5 five = v × 1 7 = 7 × 1 | |
Write the numbers as the products of prime factors.
Cancel the numbers mutual in numerator and denominator.
Therefore, \(\frac{9}{10}\) × \(\frac{2}{5}\) × \(\frac{3}{seven}\) = \(\frac{3 × three × \not 2 × 1 × 3 × i}{\not ii × five × 5 × ane × 7 × i}\)
= \(\frac{27}{175}\)
(v) Multiply \(\frac{4}{seven}\), \(\frac{three}{xi}\) and \(\frac{five}{8}\).
Solution:
To multiply 2 or more fractions, we multiply the numerators of given fractions to find the new numerator of the product and multiply the denominators to get the denominator of the product.
Hence, \(\frac{4}{vii}\) × \(\frac{3}{11}\) × \(\frac{five}{8}\) = \(\frac{four × 3 × 5}{7 × xi × eight}\)
= \(\frac{lx}{616}\)
| (vi) Multiply \(\frac{ten}{21}\) × \(\frac{5}{24}\) × \(\frac{iii}{50}\) \(\frac{10}{21}\) × \(\frac{v}{24}\) × \(\frac{iii}{50}\) =\(\frac{x × v × 3}{21 × 24 × l}\) = \(\frac{\non two × \not v × \non 5 × \not 3}{\non three × 7 × iii × \not 2 × two × 2 × two × \not v × \not 5}\) =\(\frac{1}{168}\) | 10 = ii × 5 v = v × 1 3 = iii × 1 21 = 3 × 7 24 = three × 2 × 2 × two 50 = two× five × five |
3. Multiplication of a Mixed Number past Another Mixed Number:
For Example:
| (i) Multiply 2 1/three by 1 ¾ Solution: 2 1/3 × 1 ¾ = seven/3 × seven/4 = 49/12 = iv 1/12 | We change the mixed numbers into improper fractions and so nosotros multiply as usual. |
| (ii) Multiply i 7/9 past three 5/11 Solution: 1 7/9 × three 5/eleven = 16/9 × 38/eleven = (16 × 38)/(nine × 11) = 608/99 = 6 14/99 | Nosotros change the mixed numbers into improper fractions and and then nosotros multiply as usual. |
(iii) Multiply xi\(\frac{7}{8}\) past three\(\frac{1}{24}\)
Solution:
Let u.s. first convert mixed numbers into improper fractions.
11\(\frac{7}{viii}\) = \(\frac{11 × 8 + 7}{eight}\) = \(\frac{95}{8}\)
3\(\frac{1}{24}\) = \(\frac{3 × 24 + 1}{24}\) = \(\frac{73}{24}\)
At present, \(\frac{95}{8}\) × \(\frac{73}{24}\) = \(\frac{95 × 73}{8 × 24}\)
= \(\frac{6935}{192}\)
= 36\(\frac{23}{192}\)
(iv) Multiply 3\(\frac{1}{2}\) × 2\(\frac{1}{5}\)
| three\(\frac{ane}{ii}\) × 2\(\frac{ane}{5}\) = \(\frac{7}{two}\) × \(\frac{11}{5}\) = \(\frac{7 × 11}{ii × five}\) = \(\frac{77}{10}\) = vii\(\frac{7}{10}\) | |
Questions and Answers on Multiplying Fractions:
I. Find the product:
(i) \(\frac{five}{xix}\) × ane
(2) \(\frac{half-dozen}{7}\) × 5
(iii) \(\frac{9}{14}\) × 6
(4) \(\frac{4}{13}\) × 0
(5) \(\frac{1}{7}\) × \(\frac{5}{vi}\)
(six) 1\(\frac{ane}{x}\) × 8
(vii) \(\frac{1}{7}\) × \(\frac{8}{1}\)
(8) \(\frac{1}{3}\) × \(\frac{7}{5}\) × \(\frac{2}{nine}\)
(nine) \(\frac{four}{15}\) × \(\frac{10}{21}\)
(ten) \(\frac{one}{2}\) of 100
(xi) \(\frac{1}{3}\) of 60
(xii) \(\frac{iv}{5}\) of \(\frac{8}{11}\)
Answers:
I. (i) \(\frac{5}{19}\)
(two) four\(\frac{2}{7}\)
(three) 3\(\frac{6}{7}\)
(4) 0
(v) \(\frac{5}{42}\)
(half-dozen) 8\(\frac{4}{5}\)
(vii) 1\(\frac{1}{seven}\)
(eight) \(\frac{fourteen}{135}\)
(nine) \(\frac{8}{63}\)
(ten) 50
(xi) 20
(xii) \(\frac{32}{55}\)
Two. Multiply and write the product in lowest terms.
(i) \(\frac{1}{2}\) × 40
(ii) \(\frac{1}{3}\) × 150
(iii) \(\frac{2}{seven}\) × 21
(iv) \(\frac{7}{38}\) × 0
(5) \(\frac{31}{65}\) × ane
(vi) 8 × \(\frac{17}{24}\)
(vii) \(\frac{three}{7}\) × \(\frac{vii}{15}\)
(8) \(\frac{9}{32}\) × \(\frac{8}{36}\)
(ix) \(\frac{eleven}{15}\) × \(\frac{45}{88}\)
(x) \(\frac{ii}{ten}\) ×\(\frac{3}{22}\) ×\(\frac{twoscore}{30}\)
(xi) \(\frac{1}{6}\) ×\(\frac{ii}{5}\) ×\(\frac{iii}{iv}\)
(xii) 3\(\frac{i}{7}\) ×\(\frac{21}{44}\)
Answers:
II. (i) 20
(ii) fifty
(three) half dozen
(four) 0
(v) \(\frac{31}{65}\)
(6) \(\frac{17}{3}\)
(vii) \(\frac{1}{v}\)
(viii) \(\frac{1}{xvi}\)
(ix) \(\frac{3}{eight}\)
(10) \(\frac{2}{55}\)
(eleven) \(\frac{ane}{twenty}\)
(xii) 1\(\frac{one}{2}\)
3. Discover the Product and Reduce it the Lowest Terms:
(i) 4\(\frac{1}{iii}\) × 2\(\frac{1}{3}\)
(2) six × v\(\frac{1}{ii}\)
(three) 1\(\frac{1}{7}\) × 2\(\frac{1}{4}\)
(4) \(\frac{3}{4}\) × \(\frac{ane}{three}\) × \(\frac{ii}{vi}\)
(v) 1\(\frac{one}{two}\) × 5\(\frac{2}{three}\) × 4\(\frac{i}{v}\)
(vi) \(\frac{vii}{9}\) × \(\frac{10}{15}\) × \(\frac{3}{21}\)
(vii) \(\frac{16}{48}\) × \(\frac{12}{24}\) × \(\frac{fifteen}{xxx}\)
(eight) \(\frac{19}{38}\) × \(\frac{2}{4}\) × \(\frac{8}{20}\)
(ix) \(\frac{vi}{42}\) × one\(\frac{i}{five}\) × \(\frac{xv}{fifty}\)
Answer:
III.(i) 10\(\frac{1}{9}\)
(ii) 33
(iii) two\(\frac{4}{seven}\)
(iv) \(\frac{1}{12}\)
(v) 35\(\frac{7}{x}\)
(vi) \(\frac{2}{27}\)
(vii) \(\frac{1}{12}\)
(viii) \(\frac{1}{ten}\)
(ix) \(\frac{9}{175}\)
IV. Simplify. (employ Prime Factorisation)
(i) \(\frac{7}{9}\) × \(\frac{18}{21}\) × \(\frac{6}{10}\)
(two) \(\frac{24}{36}\) × \(\frac{81}{27}\) × \(\frac{5}{10}\)
(iii) \(\frac{x}{12}\) × \(\frac{12}{14}\) × \(\frac{14}{twenty}\)
(iv) \(\frac{xv}{16}\) × \(\frac{32}{30}\) × \(\frac{one}{4}\)
(five) \(\frac{one}{2}\) × \(\frac{4}{8}\) × \(\frac{16}{6}\)
(half dozen) \(\frac{13}{22}\) × \(\frac{xi}{26}\) × \(\frac{4}{half-dozen}\)
Answer:
Iv. (i) \(\frac{2}{5}\)
(ii) 1
(iii) \(\frac{ane}{2}\)
(four) \(\frac{1}{4}\)
(five) \(\frac{two}{3}\)
(half dozen) \(\frac{1}{6}\)
V. Multiply:
(i) iv × \(\frac{six}{11}\)
(two) \(\frac{8}{thirteen}\) × 3
(iii) \(\frac{2}{v}\) × 10
(four) \(\frac{5}{7}\) × 5
(five) 8 × \(\frac{v}{6}\)
(vi) \(\frac{7}{12}\) × 2
(seven) 15 × \(\frac{1}{4}\)
(viii) 19 × \(\frac{1}{3}\)
Respond:
5. (i) 2\(\frac{two}{11}\)
(ii) 1\(\frac{eleven}{13}\)
(3) 4
(4) three\(\frac{4}{seven}\)
(five) 6\(\frac{two}{3}\)
(vi) i\(\frac{ane}{6}\)
(vii) 3\(\frac{3}{4}\)
(viii) 6\(\frac{one}{iii}\)
VI. Find the given quantity.
(i) \(\frac{1}{7}\) of 28 kg apples
(ii) \(\frac{2}{15}\) of $300
(iii) \(\frac{v}{9}\) of 54 km
(iv) \(\frac{2}{5}\) of 70 chairs
Answers:
Vi. (i) 4 kg apples
(ii) $40
(three) xxx km
(iv) 28 chairs

Seven: Word issues on Multiplying Fractions:
1. 2\(\frac{ane}{5}\) m of fabric is required to make a shirt. Ron wants to make 25 shirts, what length of cloth does he need?
Answer: 55 grand of material
two. \(\frac{3}{4}\) cups of milk is required to brand a block of ane kg. How many cups of milk is required to make a cake of 4\(\frac{one}{2}\) kg?
Answer: 3\(\frac{3}{8}\) cups
3. Shelly bought 16\(\frac{3}{4}\) liters of juice. If the cost of 1 liter juice is $8, detect the total toll of juice?
Answer: $134
4. The weight of each bag is 4\(\frac{1}{4}\) Kg. What would exist the weight of 36 such bags?
Answer: 153 kg
five. Sam works for six\(\frac{2}{8}\) hours each day. For how much time will she work in a calendar month if she works for 24 days in a month?
Respond: 150 hours
●Related Concepts
- Fraction of a Whole Numbers
- Representation of a Fraction
- Equivalent Fractions
- Properties of Equivalent Fractions
- Finding Equivalent Fractions
- Reducing the Equivalent Fractions
- Verification of Equivalent Fractions
- Finding a Fraction of a Whole Number
- Like and Unlike Fractions
- Comparison of Like Fractions
- Comparison of Fractions having the same Numerator
- Comparison of Dissimilar Fractions
- Fractions in Ascending Social club
- Fractions in Descending Guild
- Types of Fractions
- Changing Fractions
- Conversion of Fractions into Fractions having Aforementioned Denominator
- Conversion of a Fraction into its Smallest and Simplest Class
- Add-on of Fractions having the Same Denominator
- Addition of Unlike Fractions
- Addition of Mixed Fractions
- Discussion Problems on Addition of Mixed Fractions
- Worksheet on Word Problems on Improver of Mixed Fractions
- Subtraction of Fractions having the Same Denominator
- Subtraction of Different Fractions
- Subtraction of Mixed Fractions
- Word Issues on Subtraction of Mixed Fractions
- Worksheet on Give-and-take Problems on subtraction of Mixed Fractions
- Addition and Subtraction of Fractions on the Fraction Number Line
- Word Issues on Multiplication of Mixed Fractions
- Worksheet on Word Problems on Multiplication of Mixed Fractions
- Multiplying Fractions
- Dividing Fractions
- Discussion Bug on Division of Mixed Fractions
- Worksheet on Discussion Problems on Division of Mixed Fractions
4th Class Math Activities
From Multiplying Fractions to HOME Folio
Didn't find what you were looking for? Or want to know more than information most Math But Math. Employ this Google Search to discover what you need.
What Is 6/7 - 2/5,
Source: https://www.math-only-math.com/multiplying-fractions.html
Posted by: smithtrate1937.blogspot.com

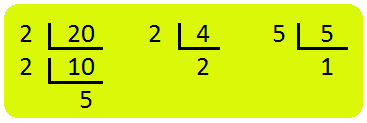

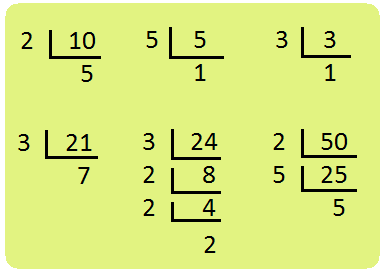
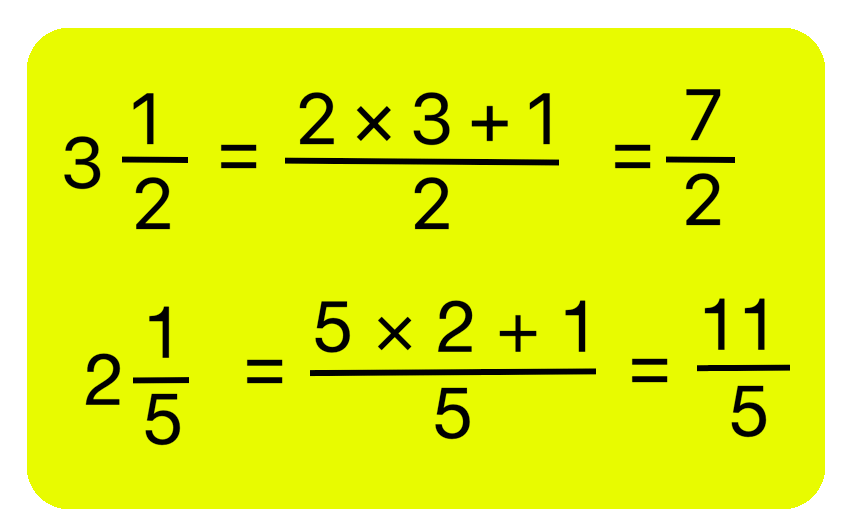

0 Response to "What Is 6/7 - 2/5"
Post a Comment